Step by Step Chi Square Test with Crosstabs in SPSS Complete
Step by Step Chi Square Test with Crosstabs in SPSS Complete | Chi square test aims to see the relationship between independent variables to the dependent variable. To perform chi square test in SPSS we can use crosstabs facility. The crosstabs command is useful for displaying contingency tables that indicate a shared distribution, description of bivariate statistics, and also to know whether there is a relationship between independent variables with dependent variables.
PROCEDURES OF USE OF CHI SQUARE TESTS
The use of chi square test to analyze data has several requirements that must be fulfilled, among others:
GUIDELINES FOR DECISION MAKING IN CHI SQUARE TEST
To detect whether there is a relationship between independent variables to the dependent variable in the chi square test, then we can refer to the decision-making guidelines below.
EXAMPLE OF CHI SQUARE TEST CASE
In the discussion of this post, we will test whether there is a relationship between variables of hypertension to obesistas variable. For research data can be seen in the picture below.
For purposes of analysis then this data should we convert into numbers, after converted then the result as follows.
Information:
hypertension = 1
not hypertension = 2
obesity = 1
not obesity = 2
For the number of samples I use as many as 50 respondents. To practice please download research data | DOWNLOAD DATA
STEP BY STEP CHI SQUARE TEST WITH CROSSTABS IN SPSS COMPLETE
To perform chi square test in SPSS, starting from entering data then analyzing data. The steps as follows.
1. Open a new worksheet by click File - New - Data, then click Variable View.
2. The next step is to enter the name and property variable.
First Variable: Hypertension, then fill.
Name: type Hypertension
Type: select numeric
Decimals: type 0 means no decimal
Width: select 2
Label: type Hypertension
Value: this option is for the coding process. Click the small box to the right of the cell. On-screen:
Charging:
Value: type 1
Label: type Hypertension
Click Add
Value: type 2
Label: Type No Hypertension
Click Add
Click Ok
Missing: select None
Columns: type 8
Align: select Right
Measure: select Nominal
Role: select Input
The second variable: Obesity, then fill.
Name: type Obesity
Type: select numeric
Decimals: type 0
Width: select 2
Label: type Obesity
Value: this option is for the coding process. Click the small box to the right of the cell.
Charging:
Value: type 1
Label: type Obesity
Click Add
Value: type 2
Label: Type No Obesity
Click Add
Click Ok
Missing: select None
Columns: type 8
Align: select Right
Measure: select Nominal
Role: select Input
Then the screen will appear as shown below
3. Next is fill 50 data hypertension and obesity. For that, return it to Data View mode. Fill in the data so it will look like the following.
4. Next we go into data processing, first click menu Analyze - Descriptive Statistics - Crosstabs ...
5. Then move the Hypertension variable to the Column(s) box, and move the Obesity variable to the Row(s) box, as shown on the screen as follows:
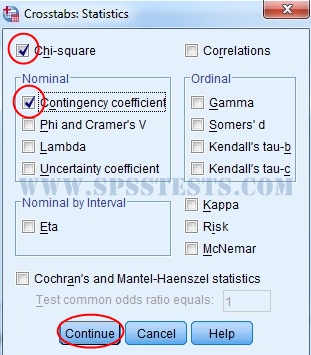
6. Click Statistics, then select Chi-Square, and select Contingency Coefficient, then click Continue
7. Next click Cells, select Observer, Expected, and Row, then click Continue
8. The final step click Ok
INTERPRETATION OF CHI SQUARE TESTS IN SPSS OUTPUT
Case Processing Summary – OUTPUT
The output of the first part states that all the valid data is 100% or 50 samples for the Crosstab process.
Obesity * Hypertension Crosstabulation – OUTPUT
Next we can see 2x2 cross tabulation between obesity with hypertension. In the picture, the box I circled in red is the expected value for each box. Nothing is worth <1 or <5. Therefore, the procedure has been met for Chi Square test.
For the values I circled blue, it shows the proportion of obese variables with hypertension higher than non-hypertensive obesity. Then, the proportion is not obese but hypertension is less than non-obese and hypertensive. Is the proportion significantly different? Then we have to see the results of the chi-squarenya test, and detect what the significance is.
Chi-Square Tests- OUTPUT
In the picture above shows 0 cells (0,%) with the expected value <5 means the cells whose expected value is below 5 by 0%. Then the minimum expected value of 11.04 means there is no expected value <1. Then the Chi-Square test procedure has been fulfilled. Based on the above output, the Sig value is obtained. (2-sided) <0,05, therefore it can be concluded that Obesity variable correlated significantly to hypertension variable.
Symmetric Measures-OUTPUT
In the Symetric Measures table, we can see the Contingency coefficient (r) is 0.375 with Approx value. Sig = 0.004. The correlation (r) is used when the variable relationship is significant (Approx .sig. <0.05). To see the level of closeness of relationships between variables can be guided by the criteria below.
Interpretation of value r. The value of r ranges from 0-1.
0 = No correlation between variables
> 0 - 0.25 = The correlation is very weak
> 0.25 - 0.5 = Correlation is enough
> 0.5 - 0.75 = Strong correlation
> 0.75 - 0.99 = Very strong correlation
1 = Perfect correlation
The r value obtained from the correlation test = 0.375. So it can be concluded: obesity is associated with the incidence of hypertension with sufficient correlation. Because the correlation value is positive then, the correlation direction is positive, it means that the more obese people will increase the hypertension.
Thus the discussion about Step by Step Chi Square Test with Crosstabs in SPSS Complete may be useful.
[Keyword: Step by Step Chi Square Test with Crosstabs in SPSS Complete, Chi Square Test With SPSS Interpretation, Interpretation of Chi Square Test Results in SPSS]
PROCEDURES OF USE OF CHI SQUARE TESTS
The use of chi square test to analyze data has several requirements that must be fulfilled, among others:
- Use of crosstabs for nominal data or category data.
- Chi square test was used in unpaired group.
- No cell can have expected value <1.
- No cell can have expected value <5 more than 20% of total cell.
GUIDELINES FOR DECISION MAKING IN CHI SQUARE TEST
To detect whether there is a relationship between independent variables to the dependent variable in the chi square test, then we can refer to the decision-making guidelines below.
- If the value of Asymp. Sig. (2-sided) <0.05 then there is a correlation.
- If the value of Asymp. Sig. (2-sided)> 0.05 then there is no correlation.
EXAMPLE OF CHI SQUARE TEST CASE
In the discussion of this post, we will test whether there is a relationship between variables of hypertension to obesistas variable. For research data can be seen in the picture below.
For purposes of analysis then this data should we convert into numbers, after converted then the result as follows.
Information:
hypertension = 1
not hypertension = 2
obesity = 1
not obesity = 2
For the number of samples I use as many as 50 respondents. To practice please download research data | DOWNLOAD DATA
STEP BY STEP CHI SQUARE TEST WITH CROSSTABS IN SPSS COMPLETE
To perform chi square test in SPSS, starting from entering data then analyzing data. The steps as follows.
1. Open a new worksheet by click File - New - Data, then click Variable View.
2. The next step is to enter the name and property variable.
First Variable: Hypertension, then fill.
Name: type Hypertension
Type: select numeric
Decimals: type 0 means no decimal
Width: select 2
Label: type Hypertension
Value: this option is for the coding process. Click the small box to the right of the cell. On-screen:
Charging:
Value: type 1
Label: type Hypertension
Click Add
Value: type 2
Label: Type No Hypertension
Click Add
Click Ok
Missing: select None
Columns: type 8
Align: select Right
Measure: select Nominal
Role: select Input
The second variable: Obesity, then fill.
Name: type Obesity
Type: select numeric
Decimals: type 0
Width: select 2
Label: type Obesity
Value: this option is for the coding process. Click the small box to the right of the cell.
Charging:
Value: type 1
Label: type Obesity
Click Add
Value: type 2
Label: Type No Obesity
Click Add
Click Ok
Missing: select None
Columns: type 8
Align: select Right
Measure: select Nominal
Role: select Input
Then the screen will appear as shown below
3. Next is fill 50 data hypertension and obesity. For that, return it to Data View mode. Fill in the data so it will look like the following.
4. Next we go into data processing, first click menu Analyze - Descriptive Statistics - Crosstabs ...
5. Then move the Hypertension variable to the Column(s) box, and move the Obesity variable to the Row(s) box, as shown on the screen as follows:
6. Click Statistics, then select Chi-Square, and select Contingency Coefficient, then click Continue
7. Next click Cells, select Observer, Expected, and Row, then click Continue
8. The final step click Ok
INTERPRETATION OF CHI SQUARE TESTS IN SPSS OUTPUT
Case Processing Summary – OUTPUT
The output of the first part states that all the valid data is 100% or 50 samples for the Crosstab process.
Obesity * Hypertension Crosstabulation – OUTPUT
Next we can see 2x2 cross tabulation between obesity with hypertension. In the picture, the box I circled in red is the expected value for each box. Nothing is worth <1 or <5. Therefore, the procedure has been met for Chi Square test.
For the values I circled blue, it shows the proportion of obese variables with hypertension higher than non-hypertensive obesity. Then, the proportion is not obese but hypertension is less than non-obese and hypertensive. Is the proportion significantly different? Then we have to see the results of the chi-squarenya test, and detect what the significance is.
Chi-Square Tests- OUTPUT
In the picture above shows 0 cells (0,%) with the expected value <5 means the cells whose expected value is below 5 by 0%. Then the minimum expected value of 11.04 means there is no expected value <1. Then the Chi-Square test procedure has been fulfilled. Based on the above output, the Sig value is obtained. (2-sided) <0,05, therefore it can be concluded that Obesity variable correlated significantly to hypertension variable.
Symmetric Measures-OUTPUT
In the Symetric Measures table, we can see the Contingency coefficient (r) is 0.375 with Approx value. Sig = 0.004. The correlation (r) is used when the variable relationship is significant (Approx .sig. <0.05). To see the level of closeness of relationships between variables can be guided by the criteria below.
Interpretation of value r. The value of r ranges from 0-1.
0 = No correlation between variables
> 0 - 0.25 = The correlation is very weak
> 0.25 - 0.5 = Correlation is enough
> 0.5 - 0.75 = Strong correlation
> 0.75 - 0.99 = Very strong correlation
1 = Perfect correlation
The r value obtained from the correlation test = 0.375. So it can be concluded: obesity is associated with the incidence of hypertension with sufficient correlation. Because the correlation value is positive then, the correlation direction is positive, it means that the more obese people will increase the hypertension.
Thus the discussion about Step by Step Chi Square Test with Crosstabs in SPSS Complete may be useful.
~~~ Thank You ~~~
[Keyword: Step by Step Chi Square Test with Crosstabs in SPSS Complete, Chi Square Test With SPSS Interpretation, Interpretation of Chi Square Test Results in SPSS]















This is the best site for learning. Thank you admin
ReplyDelete